Minimum Time to Make Rope Colorful

 Alice has n balloons arranged on a rope. You are given a 0-indexed string colors where colors[i] is the color of the ith balloon.

Alice wants the rope to be colorful. She does not want two consecutive balloons to be of the same color, so she asks Bob for help. Bob can remove some balloons from the rope to make it colorful. You are given a 0-indexed integer array neededTime where neededTime[i] is the time (in seconds) that Bob needs to remove the ith balloon from the rope.

Return the minimum time Bob needs to make the rope colorful.

 

Example 1:

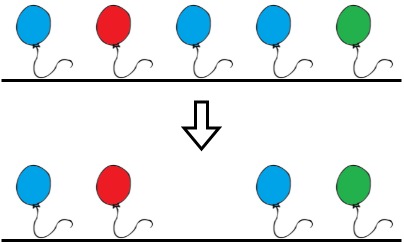
Input: colors = "abaac", neededTime = [1,2,3,4,5]
Output: 3
Explanation: In the above image, 'a' is blue, 'b' is red, and 'c' is green.
Bob can remove the blue balloon at index 2. This takes 3 seconds.
There are no longer two consecutive balloons of the same color. Total time = 3.

Example 2:

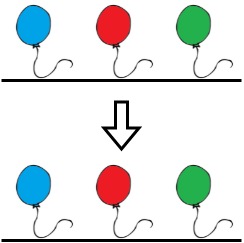
Input: colors = "abc", neededTime = [1,2,3]
Output: 0
Explanation: The rope is already colorful. Bob does not need to remove any balloons from the rope.

Example 3:

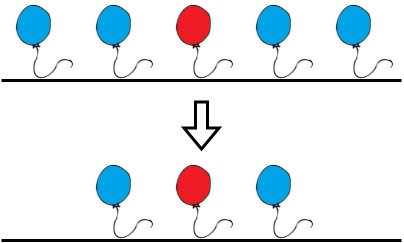
Input: colors = "aabaa", neededTime = [1,2,3,4,1]
Output: 2
Explanation: Bob will remove the ballons at indices 0 and 4. Each ballon takes 1 second to remove.
There are no longer two consecutive balloons of the same color. Total time = 1 + 1 = 2.

 

Constraints:

• n == colors.length == neededTime.length
• 1 <= n <= 105
• 1 <= neededTime[i] <= 104

class Solution {
    public int minCost(String colors, int[] neededTime) {
        int minTime = 0;
        int n = colors.length();
        int max_time = 0;
        int total_sum = 0;
        for(int i=0;i<n;i++){
            if(i>0 && colors.charAt(i) != colors.charAt(i-1)){
                minTime += total_sum - max_time;
                total_sum = max_time = 0;
            }
            total_sum += neededTime[i];
            max_time = Math.max(max_time,neededTime[i]);
        }
        minTime += (total_sum - max_time);
        return minTime;
    }
}

TC : O(N) SC:O(1)

Maximal Network Rank

 There is an infrastructure of n cities with some number of roads connecting these cities. Each roads[i] = [ai, bi] indicates that there is a bidirectional road between cities ai and bi.

The network rank of two different cities is defined as the total number of directly connected roads to either city. If a road is directly connected to both cities, it is only counted once.

The maximal network rank of the infrastructure is the maximum network rank of all pairs of different cities.

Given the integer n and the array roads, return the maximal network rank of the entire infrastructure.

 

Example 1:

Input: n = 4, roads = [[0,1],[0,3],[1,2],[1,3]]
Output: 4
Explanation: The network rank of cities 0 and 1 is 4 as there are 4 roads that are connected to either 0 or 1. The road between 0 and 1 is only counted once.

Example 2:

Input: n = 5, roads = [[0,1],[0,3],[1,2],[1,3],[2,3],[2,4]]
Output: 5
Explanation: There are 5 roads that are connected to cities 1 or 2.

Example 3:

Input: n = 8, roads = [[0,1],[1,2],[2,3],[2,4],[5,6],[5,7]]
Output: 5
Explanation: The network rank of 2 and 5 is 5. Notice that all the cities do not have to be connected.

 

Constraints:

• 2 <= n <= 100
• 0 <= roads.length <= n * (n - 1) / 2
• roads[i].length == 2
• 0 <= ai, bi <= n-1
• ai != bi
• Each pair of cities has at most one road connecting them.

class Solution {
    public int maximalNetworkRank(int n, int[][] roads) {
        boolean [][] connected = new boolean[n][n];
        int [] count = new int[n];
        int maxNetworkRank = 0;
        for( int [] road : roads){
            count[road[0]]++;
            count[road[1]]++;
            connected[road[0]][road[1]] = true;
            connected[road[1]][road[0]] = true;
        }
        
        for(int i=0;i<n;i++){
            for(int j = i+1;j<n;j++){
                maxNetworkRank = Math.max(maxNetworkRank, count[i]+count[j] - (connected[i][j] ? 1 : 0));
            }
        }
        
        return maxNetworkRank;
    
    }
}

TC 

TC : O(N*N) SC : O(N)

Minimum Deletions to Make Character Frequencies Unique

 A string s is called good if there are no two different characters in s that have the same frequency.

Given a string s, return the minimum number of characters you need to delete to make s good.

The frequency of a character in a string is the number of times it appears in the string. For example, in the string "aab", the frequency of 'a' is 2, while the frequency of 'b' is 1.

 

Example 1:

Input: s = "aab"
Output: 0
Explanation: s is already good.

Example 2:

Input: s = "aaabbbcc"
Output: 2
Explanation: You can delete two 'b's resulting in the good string "aaabcc".
Another way it to delete one 'b' and one 'c' resulting in the good string "aaabbc".

Example 3:

Input: s = "ceabaacb"
Output: 2
Explanation: You can delete both 'c's resulting in the good string "eabaab".
Note that we only care about characters that are still in the string at the end (i.e. frequency of 0 is ignored).

class Solution {
  public int minDeletions(String s) {
       int [] freqCount = new int[26];
       for(char ch:s.toCharArray()){
           freqCount[ch-'a']++;
       }
       Set<Integer> seenFrequency = new HashSet<>();
      int minDeletions = 0;
       for(int i=0;i< 26;i++){
           while(freqCount[i] > 0){
               if(!seenFrequency.contains(freqCount[i])){
                   seenFrequency.add(freqCount[i]);
                   break;
               }
               freqCount[i]--;
               minDeletions++;
           }
       }       
      return minDeletions;
    }
}
TC : O(1)
SC : O(1)

Design HashMap

Design a HashMap without using any built-in hash table libraries.

Implement the MyHashMap class:

• MyHashMap() initializes the object with an empty map.
• void put(int key, int value) inserts a (key, value) pair into the HashMap. If the key already exists in the map, update the corresponding value.
• int get(int key) returns the value to which the specified key is mapped, or -1 if this map contains no mapping for the key.
• void remove(key) removes the key and its corresponding value if the map contains the mapping for the key.

 

Example 1:

Input
["MyHashMap", "put", "put", "get", "get", "put", "get", "remove", "get"]
[[], [1, 1], [2, 2], [1], [3], [2, 1], [2], [2], [2]]
Output
[null, null, null, 1, -1, null, 1, null, -1]

Explanation
MyHashMap myHashMap = new MyHashMap();
myHashMap.put(1, 1); // The map is now [[1,1]]
myHashMap.put(2, 2); // The map is now [[1,1], [2,2]]
myHashMap.get(1);    // return 1, The map is now [[1,1], [2,2]]
myHashMap.get(3);    // return -1 (i.e., not found), The map is now [[1,1], [2,2]]
myHashMap.put(2, 1); // The map is now [[1,1], [2,1]] (i.e., update the existing value)
myHashMap.get(2);    // return 1, The map is now [[1,1], [2,1]]
myHashMap.remove(2); // remove the mapping for 2, The map is now [[1,1]]
myHashMap.get(2);    // return -1 (i.e., not found), The map is now [[1,1]]

 

Constraints:

• 0 <= key, value <= 106
• At most 104 calls will be made to put, get, and remove.

class Pair<U,V>{
    public U first;
    public V second;
    public Pair(U first, V second){
        this.first = first;
        this.second = second;
    }
}

class Bucket{
    private List<Pair<Integer,Integer>> bucket;
    public Bucket(){
        this.bucket = new LinkedList<Pair<Integer,Integer>>();
    }
    
    public Integer get(Integer key){
        for(Pair<Integer,Integer> pair:this.bucket){
            if(pair.first.equals(key)){
                return pair.second;
            }
        }
        return -1;
    }
    
    public void update(Integer key,Integer value){
        boolean isFound = false;
        for(Pair<Integer,Integer> pair:this.bucket){
            if(pair.first.equals(key)){
                isFound = true;
                pair.second = value;
            }
        }
        if(!isFound){
            this.bucket.add(new Pair<Integer,Integer>(key,value));
        }
    }
    
    public void remove(Integer key){
        for(Pair<Integer,Integer> pair : this.bucket){
            if(pair.first.equals(key)){
                this.bucket.remove(pair);
                break;
            }
        }
    }
}



class MyHashMap {
    private int key_space;
    private List<Bucket> hash_table;

    public MyHashMap() {
        this.key_space = 2069;
        this.hash_table = new ArrayList<Bucket>();
        for(int i =0;i<key_space;i++){
            this.hash_table.add(new Bucket());
        }
    }
    
    public void put(int key, int value) {
        int hash_key = key % this.key_space;
        this.hash_table.get(hash_key).update(key,value);
    }
    
    public int get(int key) {
        int hash_key = key % this.key_space;
        return this.hash_table.get(hash_key).get(key);
    }
    
    public void remove(int key) {
        int hash_key = key % this.key_space;
        this.hash_table.get(hash_key).remove(key);
    }
}

/**
 * Your MyHashMap object will be instantiated and called as such:
 * MyHashMap obj = new MyHashMap();
 * obj.put(key,value);
 * int param_2 = obj.get(key);
 * obj.remove(key);
 */

Complexity Analysis
Time Complexity: for each of the methods, the time complexity is $\mathcal{O}(\frac{N}{K})$ where $N$ is the number of all possible keys and $K$ is the number of predefined buckets in the hashmap, which is 2069 in our case.
In the ideal case, the keys are evenly distributed in all buckets. As a result, on average, we could consider the size of the bucket is $\frac{N}{K}$.
Since in the worst case we need to iterate through a bucket to find the desire value, the time complexity of each method is $\mathcal{O}(\frac{N}{K})$.
Space Complexity: $\mathcal{O}(K+M)$ where $K$ is the number of predefined buckets in the hashmap and $M$ is the number of unique keys that have been inserted into the hashmap.