Invert Binary Tree - Leetcode Python Solution

 Invert a binary tree.

Example:

Input:

     4
   /   \
  2     7
 / \   / \
1   3 6   9

Output:

     4
   /   \
  7     2
 / \   / \
9   6 3   1

Iterative approcah . 

# Definition for a binary tree node.

# class TreeNode:

#     def __init__(self, val=0, left=None, right=None):

#         self.val = val

#         self.left = left

#         self.right = right

class Solution:

    def invertTree(self, root: TreeNode) -> TreeNode:

        if not root:

            return None

        q = []

        q.append(root)

        while q:

            curr = q.pop()

            curr.left , curr.right = curr.right,curr.left

            if curr.left:

                q.append(curr.left)

            if curr.right:

                q.append(curr.right)

        return root

            

        TC: O(n)

        SC: O(n) in worst case where queue is completely occupied. 

Recursive approch:

# Definition for a binary tree node.

# class TreeNode:

#     def __init__(self, val=0, left=None, right=None):

#         self.val = val

#         self.left = left

#         self.right = right

class Solution:

    def invertTree(self, root: TreeNode) -> TreeNode:

        if not root:

            return None

        curr = root

        if curr.left:

            self.invertTree(curr.left)

        if curr.right:

            self.invertTree(curr.right)

        curr.left,curr.right = curr.right,curr.left

        return root

            

    Recursive approach:

# Definition for a binary tree node.

# class TreeNode:

#     def __init__(self, val=0, left=None, right=None):

#         self.val = val

#         self.left = left

#         self.right = right

class Solution:

    def invertTree(self, root: TreeNode) -> TreeNode:

        if not root:

            return None

        curr = root

        curr.left,curr.right = curr.right,curr.left

        if curr.left:

            self.invertTree(curr.left)

        if curr.right:

            self.invertTree(curr.right)

        return root

            

       TC: O(n)

       SC: O(n) 

Maximum Product Subarray - Python Leetcode

 Given an integer array nums, find the contiguous subarray within an array (containing at least one number) which has the largest product.

Example 1:

Input: [2,3,-2,4]
Output: 6
Explanation: [2,3] has the largest product 6.

Example 2:

Input: [-2,0,-1]
Output: 0
Explanation: The result cannot be 2, because [-2,-1] is not a subarray.

class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        if not nums:
            return 0
        
        max_so_far = nums[0]
        min_so_far = nums[0]
        result = max_so_far
        
        for i in range(1,len(nums)):
            curr = nums[i]
            temp_value = max(curr,max_so_far*curr,min_so_far*curr)
            min_so_far = min(curr,min_so_far*curr,max_so_far*curr)
            max_so_far = temp_value
            result = max(result,max_so_far)
            
        return result

TC:O(n)

SC:O(1)

Binary Tree Zigzag Level Order Traversal - Python Leetcode

 Given a binary tree, return the zigzag level order traversal of its nodes' values. (ie, from left to right, then right to left for the next level and alternate between).

For example:
Given binary tree [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

return its zigzag level order traversal as:

[
  [3],
  [20,9],
  [15,7]
]

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
from collections import deque

class Solution:
    def zigzagLevelOrder(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        if not root:
            return []
        
        s1 = [root]
        s2 = []
        
        level =[]
        result = []
        
        while s1 or s2:
            while s1:
                root = s1.pop()
                level.append(root.val)
                if root.left:
                    s2.append(root.left)
                if root.right:
                    s2.append(root.right)
            if level:
                result.append(level)
            level = []
            while s2:
                root = s2.pop()
                level.append(root.val)
                if root.right:
                    s1.append(root.right)
                if root.left:
                    s1.append(root.left)
            if level:
                result.append(level)
            level = []
        return result
                
            
    TC : O(n)

SC:O(n)

Clone Graph - LeetCode Python

 Given a reference of a node in a connected undirected graph.

Return a deep copy (clone) of the graph.

Each node in the graph contains a val (int) and a list (List[Node]) of its neighbors.

class Node {
    public int val;
    public List<Node> neighbors;
}

 

Test case format:

For simplicity sake, each node's value is the same as the node's index (1-indexed). For example, the first node with val = 1, the second node with val = 2, and so on. The graph is represented in the test case using an adjacency list.

Adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.

The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.

 

Example 1:

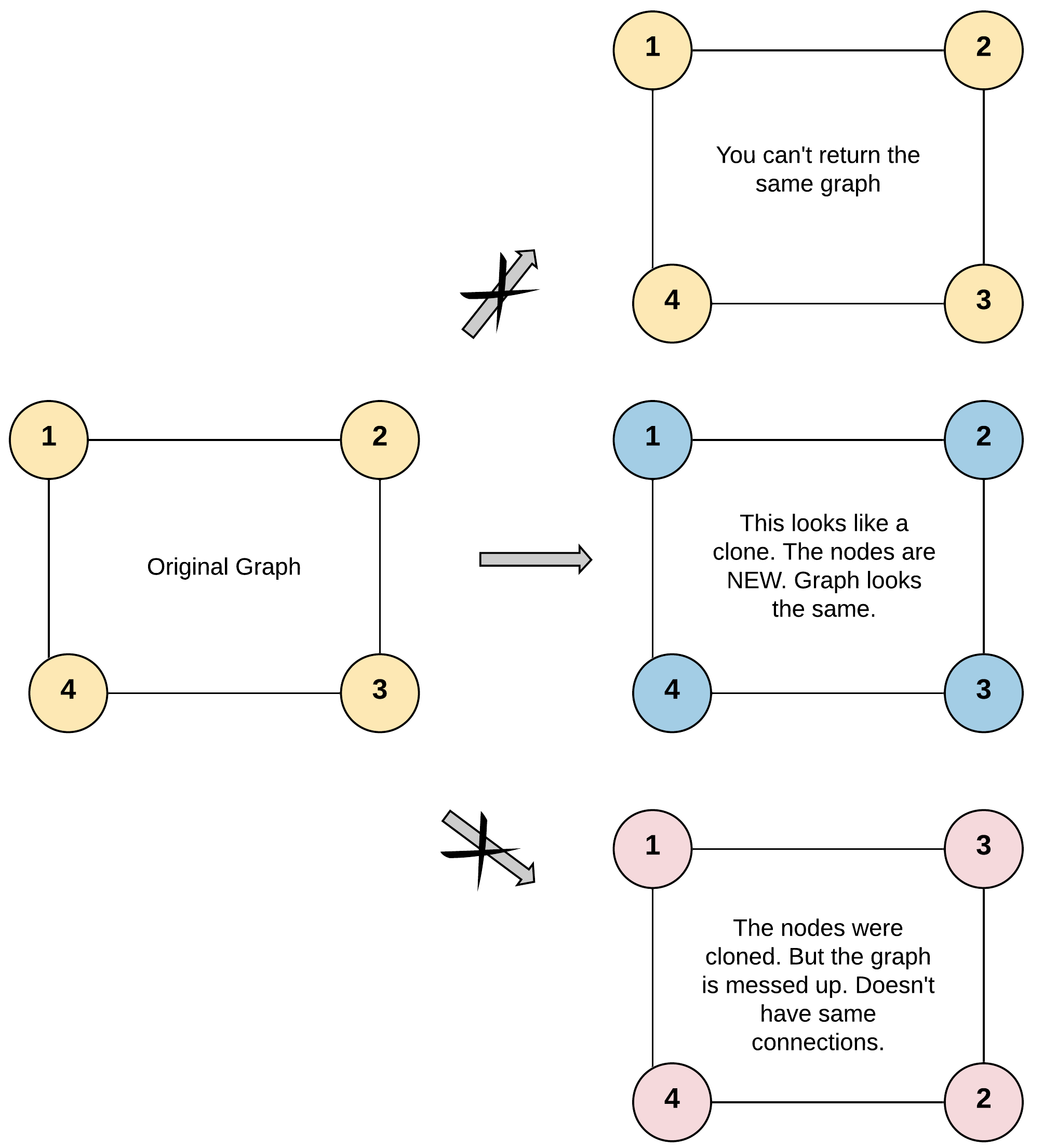
Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
Explanation: There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).

Example 2:

Input: adjList = [[]]
Output: [[]]
Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.

Example 3:

Input: adjList = []
Output: []
Explanation: This an empty graph, it does not have any nodes.

Example 4:

Input: adjList = [[2],[1]]
Output: [[2],[1]]

 

Constraints:

• 1 <= Node.val <= 100
• Node.val is unique for each node.
• Number of Nodes will not exceed 100.
• There is no repeated edges and no self-loops in the graph.
• The Graph is connected and all nodes can be visited starting from the given node.

"""

# Definition for a Node.

class Node:

    def __init__(self, val = 0, neighbors = None):

        self.val = val

        self.neighbors = neighbors if neighbors is not None else []

"""

class Solution:

    def cloneGraph(self, node: 'Node') -> 'Node':

        

        if not node:

            return

        

        visited = {}

        

        visited[node] = Node(node.val,[])

        from collections import deque

        

        queue = deque([node])

        

        while queue:

            n = queue.popleft()

            

            for neighbor in n.neighbors:

                if neighbor not in visited:

                    visited[neighbor] = Node(neighbor.val,[])

                    queue.append(neighbor)

                visited[n].neighbors.append(visited[neighbor])

        return visited[node]

        

TC : O(N)

SC: O(N)

Search a 2D Matrix II - Python Leetcode

 Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:

• Integers in each row are sorted in ascending from left to right.
• Integers in each column are sorted in ascending from top to bottom.

Example:

Consider the following matrix:

[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

Using Search Space Reduction Method

Given target = 5, return true.

Given target = 20, return false.

class Solution:

    def searchMatrix(self, matrix, target):

        """

        :type matrix: List[List[int]]

        :type target: int

        :rtype: bool

        """

        if not matrix:

            return False

        rows = len(matrix)

        cols = len(matrix[0])

        

        if rows == 0 or cols ==0:

            return False

        

        row = rows-1

        col = 0

        

        while row >=0 and col < cols:

            if target == matrix[row][col]:

                return True

            elif target < matrix[row][col]:

                row -= 1

            else:

                col+=1

        return False

        Time Complexity : O(m+n)

        Space Complexity : O(1)

Search a 2D Matrix Python Leetcode

 Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:

• Integers in each row are sorted from left to right.
• The first integer of each row is greater than the last integer of the previous row.

Example 1:

Input:
matrix = [
  [1,   3,  5,  7],
  [10, 11, 16, 20],
  [23, 30, 34, 50]
]
target = 3
Output: true

Example 2:

Input:
matrix = [
  [1,   3,  5,  7],
  [10, 11, 16, 20],
  [23, 30, 34, 50]
]
target = 13
Output: false

Main thing to note in this problem : row = pivot // cols and col = pivot % cols 

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        if not matrix or len(matrix) == 0:
            return False
        rows = len(matrix)
        cols = len(matrix[0])
        
        if rows == 1 and cols ==1:
            if target == matrix[rows-1][cols-1]:
                return True
            else:
                return False
       
        left = 0
        right = rows * cols -1
        
        while left <= right:
            pivot = left + (right-left) // 2
            
            if target == matrix[pivot // cols][pivot % cols]:
                return True
            elif target > matrix[pivot // cols][pivot % cols]:
                    left = pivot + 1
            else:
                right = pivot - 1
        return False

Time Complexity : O(logn(mn))

Space Complexity : O(1)

Search in Rotated Sorted Array - Python Leetcode

 You are given an integer array nums sorted in ascending order, and an integer target.

Suppose that nums is rotated at some pivot unknown to you beforehand (i.e., [0,1,2,4,5,6,7] might become [4,5,6,7,0,1,2]).

If target is found in the array return its index, otherwise, return -1.

 

Example 1:

Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4

Example 2:

Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1

Example 3:

Input: nums = [1], target = 0
Output: -1

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        if not nums:
            return -1
        
        if len(nums) == 1 and target == nums[0]:
            return 0
        
        left = 0
        right = len(nums)-1
        
        while left <= right:
            mid = left + (right-left) // 2
            
            if nums[mid] == target:
                return mid
            
            elif nums[mid] >= nums[left]:
                if target < nums[mid] and target >= nums[left]:
                    right = mid - 1
                else:
                    left = mid + 1
            else:
                if target > nums[mid] and target <= nums[right]:
                    left = mid + 1
                else:
                    right = mid - 1
        return -1
        

Complexity Analysis
Time complexity: $\mathcal{O}(\log{N})$.
Space complexity: $\mathcal{O}(1)$.