Tic-tac-toe is played by two players A and B on a 3 x 3 grid. The rules of Tic-Tac-Toe are:
- Players take turns placing characters into empty squares
' '. - The first player
Aalways places'X'characters, while the second playerBalways places'O'characters. 'X'and'O'characters are always placed into empty squares, never on filled ones.- The game ends when there are three of the same (non-empty) character filling any row, column, or diagonal.
- The game also ends if all squares are non-empty.
- No more moves can be played if the game is over.
Given a 2D integer array moves where moves[i] = [rowi, coli] indicates that the ith move will be played on grid[rowi][coli]. return the winner of the game if it exists (A or B). In case the game ends in a draw return "Draw". If there are still movements to play return "Pending".
You can assume that moves is valid (i.e., it follows the rules of Tic-Tac-Toe), the grid is initially empty, and A will play first.
Example 1:
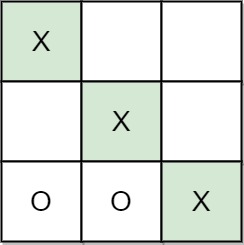
Input: moves = [[0,0],[2,0],[1,1],[2,1],[2,2]] Output: "A" Explanation: A wins, they always play first.
Example 2:
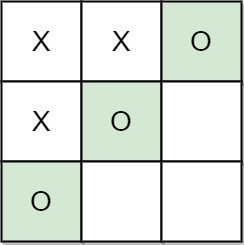
Input: moves = [[0,0],[1,1],[0,1],[0,2],[1,0],[2,0]] Output: "B" Explanation: B wins.
Example 3:
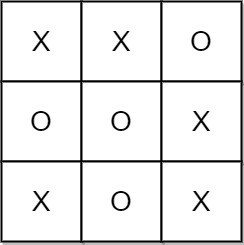
Input: moves = [[0,0],[1,1],[2,0],[1,0],[1,2],[2,1],[0,1],[0,2],[2,2]] Output: "Draw" Explanation: The game ends in a draw since there are no moves to make.
Constraints:
1 <= moves.length <= 9moves[i].length == 20 <= rowi, coli <= 2- There are no repeated elements on
moves. movesfollow the rules of tic tac toe.
class Solution {
public String tictactoe(int[][] moves) {
int n = 3;
int[] rows = new int[n];
int[] cols = new int[n];
int player = 1;
int diag = 0;
int antidiag = 0;
for(int[] move:moves){
int row = move[0];
int col = move[1];
rows[row] += player;
cols[col] += player;
if(row == col){
diag+= player;
}
if(row + col == n-1){
antidiag += player;
}
if(Math.abs(diag) == n || Math.abs(antidiag) == n || Math.abs(rows[row]) == n || Math.abs(cols[col]) == n){
return player == 1 ? "A":"B";
}
player *= -1;
}
return moves.length == n * n ? "Draw" : "Pending";
}
}Time complexity:
For every move, we update the value for a row, column, diagonal, and anti-diagonal. Each update takes constant time. We also check if any of these lines satisfies the winning condition which also takes constant time.
Space complexity:
We use two arrays of size
nto record the value for each row and column, and two integers of constant space to record to value for diagonal and anti-diagonal.
